Gossip 原理简介
- Gossip,中文为流言蜚语的意思, Gossip protocol 也叫流言算法,此协议的作用和其名字表示的意思相同。Bitcoin 使用了 gossip 算法来传播交易和区块信息
- Gossip protocol 最早是在 1987 年发表在 ACM 上的论文 《Epidemic Algorithms for Replicated Database Maintenance》中被提出。主要用在分布式数据库系统中各个副本节点同步数据之用,这种场景的一个最大特点就是组成的网络的节点都是对等节点,是非结构化网络,这区别于用于结构化网络中的 DHT 算法 Kadmelia。
- Gossip 的执行过程如下动图所示:
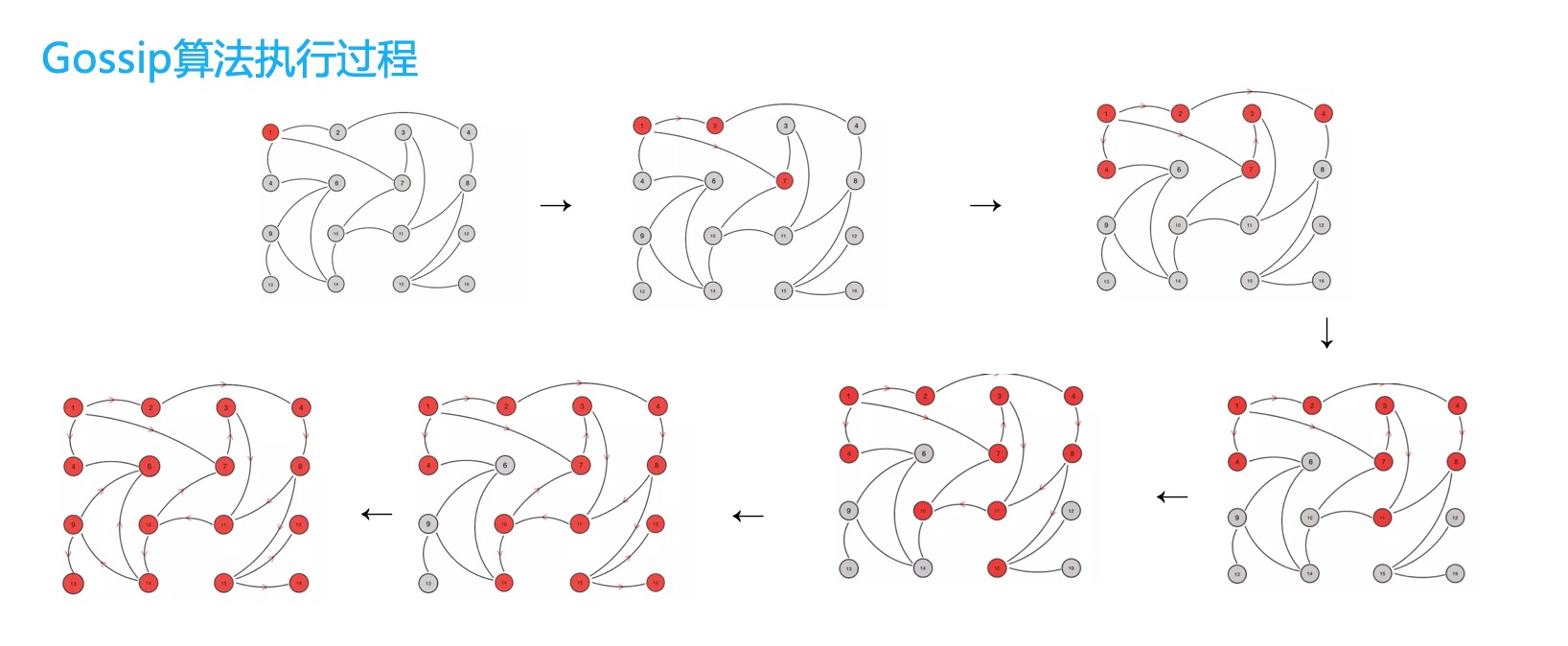
Gossip 分类
Anti-Entropy(反熵):
Anti-Entropy 以固定的概率传播
所有的数据Anti-Entropy 是
SI model(下文有介绍),节点只有两种状态:Suspective和Infective,称为 simple epidemics。之所以叫
反熵,是因为 entropy 是指混乱程度(disorder),而在这种模式下可以消除不同节点中数据的 disorder,因此 anti-entropy 就是 anti-disorder (它可以提高系统中节点之间的 similarity)。在 SI model 下,一个节点会把所有的数据都跟其他节点共享,以便消除节点之间数据的任何不一致,它可以保证最终、完全的一致。由于在 SI model 下消息会不断反复的交换,因此消息数量是非常庞大的,无限制的(unbounded),这对一个系统来说是一个巨大的开销。
Rumor-Mongering(谣言传播):
仅传播新到达的数据
Rumor-Mongering 是
SIR model(下文有介绍),节点有三种状态,Suspective,Infective和Removed,称为 complex epidemics。Rumor Mongering 模型下,由于消息只包含最新的 update,并且在某个时间点之后消息不再传播,所以消息是有限的,系统开销小,因此消息可以发送得更频繁。
当一个 Rumor 消息在某个时间点之后会被标记为 removed,并且不再被传播。因此,SIR model 下,系统有一定的概率会不一致。
Gossip 的通信模式
模式一:Push
节点 A 将数据 (key,value,version) 及对应的版本号推送给 B 节点,B 节点更新 A 中比自己新的数据
模式二:Pull
A 仅将数据 key, version 推送给 B,B 将本地比 A 新的数据(Key, value, version)推送给 A,A 更新本地
模式三:Push/Pull
与 Pull 类似,只是多了一步,A 再将本地比 B 新的数据推送给 B,B 则更新本地
如果把两个节点数据同步一次定义为一个周期,则在一个周期内,Push 需通信 1 次,Pull 需 2 次,Push/Pull 则需 3 次。虽然消息数增加了,但从效果上来讲,Push/Pull 最好,理论上一个周期内可以使两个节点完全一致。直观上,Push/Pull 的收敛速度也是最快的。
Gossip 复杂度分析
对于一个节点数为 N 的网络来说,假设每个 Gossip 周期,新感染的节点都能再感染至少一个新节点,那么 Gossip 协议退化成一个二叉树查找,经过 LogN 个周期之后,感染全网,时间复杂度是 O(LogN)。由于每个周期,每个节点都会至少发出一次消息,因此,消息复杂度是 O(N^2)(消息数量 = N * N) 。注意,这是 Gossip 理论上最优的收敛速度,但是在实际情况中,最优的收敛速度是很难达到的。
节点数据同步概率计算
假设某个节点在第 i 个周期被感染的概率为 pi,第 i+1 个周期被感染的概率为 pi+1 ,
Pull:
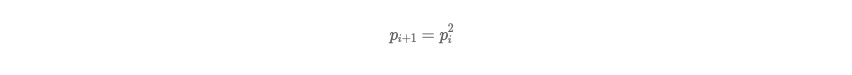
Push:
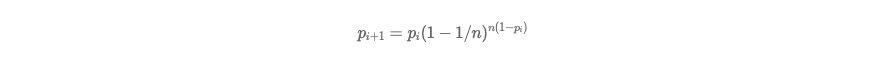
显然 Pull 的收敛速度大于 Push ,而每个节点在每个周期被感染的概率都是固定的 p (0<p<1),因此 Gossip 算法是基于 p 的平方收敛,也称为
概率收敛,这在众多的一致性算法中是非常独特的。
Gossip 的优缺点
优点:
扩展性:
网络可以允许节点的任意增加和减少,新增加的节点的状态最终会与其他节点一致。容错:
网络中任何节点的宕机和重启都不会影响 Gossip 消息的传播,Gossip 协议具有天然的分布式系统容错特性。去中心化:
Gossip 协议不要求任何中心节点,所有节点都可以是对等的,任何一个节点无需知道整个网络状况,只要网络是连通的,任意一个节点就可以把消息散播到全网。一致性收敛:
Gossip 协议中的消息会以一传十、十传百一样的指数级速度在网络中快速传播,因此系统状态的不一致可以在很快的时间内收敛到一致。消息传播速度达到了 logN。简单:
Gossip 协议的过程极其简单,实现起来几乎没有太多复杂性。
Márk Jelasity 在它的 《Gossip》一书中对其进行了归纳:
缺点:
消息延迟:
经过多次散播而达到的最终一致性,导致消息同步会延迟,不适合实时性要求高的场景消息冗余:
没有中心节点,且随机向周围节点发送消息,导致一些数据的重复传播;相比于中心节点,会消耗更多网络资源
补充: SI、SIS、SIR、SIRS、SEIR、SRIRS 模型简介
上述6种模型是传染病动力学仓室模型中最基本的6种模型,其共同特征是研究群体里至少包括两类基本人群:即易感者 S 与染病者 I。这两类人群也是所有仓室流行病模型里都必须包括的,下面会对上述模型做相应的解释。
SI 模型
SI 是传染动力学中最简单的模型,首先把人群分为2种: 易感者(Susceptibles,表示健康的人群,人数用 S 表示) 和 感染者(The Infected,人数用 I 来表示)
模型特征
假设:
1、在疾病传播期间总人数N不变,N=S+I
2、每个病人每天接触人数为定值
模型特征如下: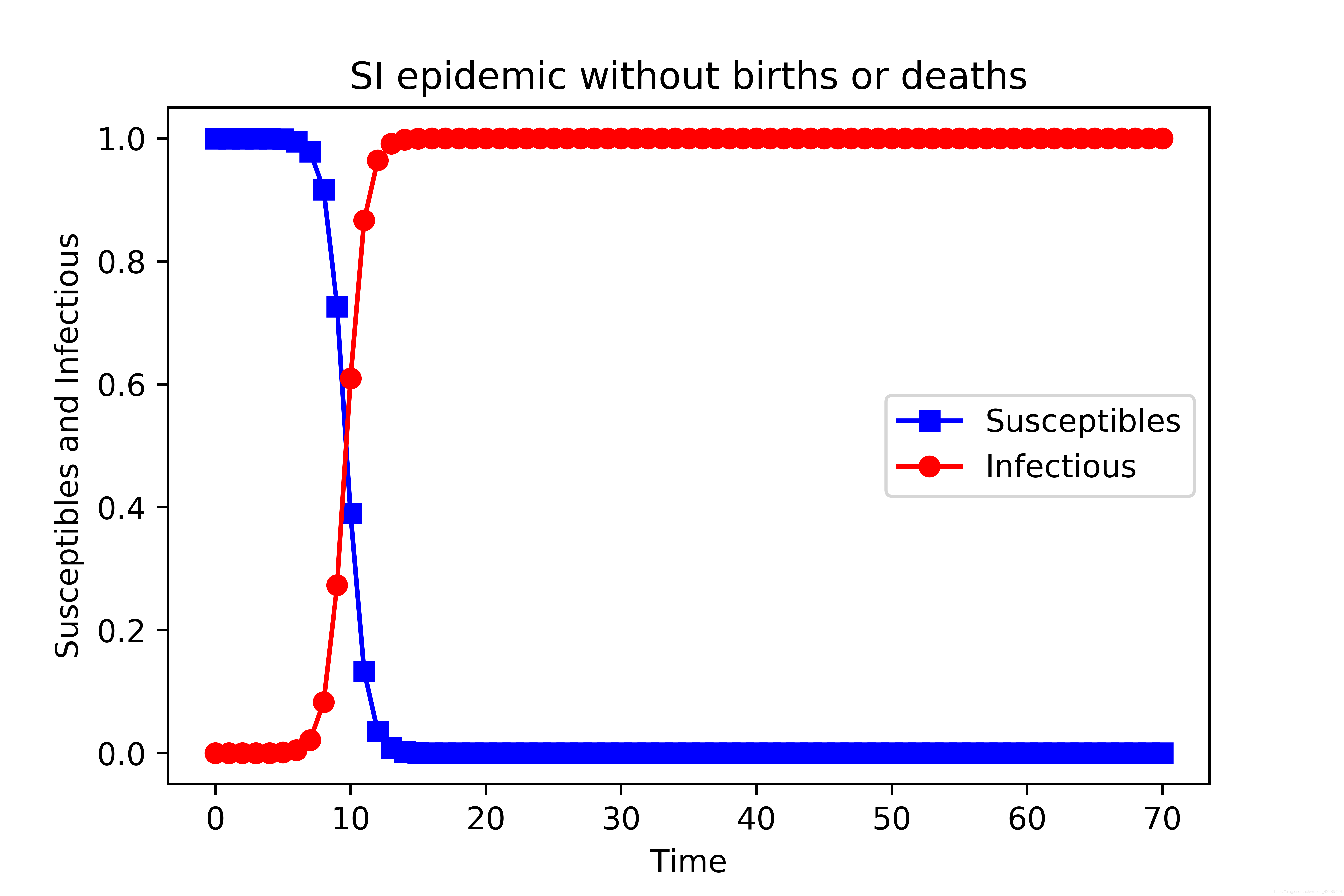
SIS 模型
在 SI 模型基础上加入康复的概率, 但是会存在重复感染
模型特征
模型特如下所示: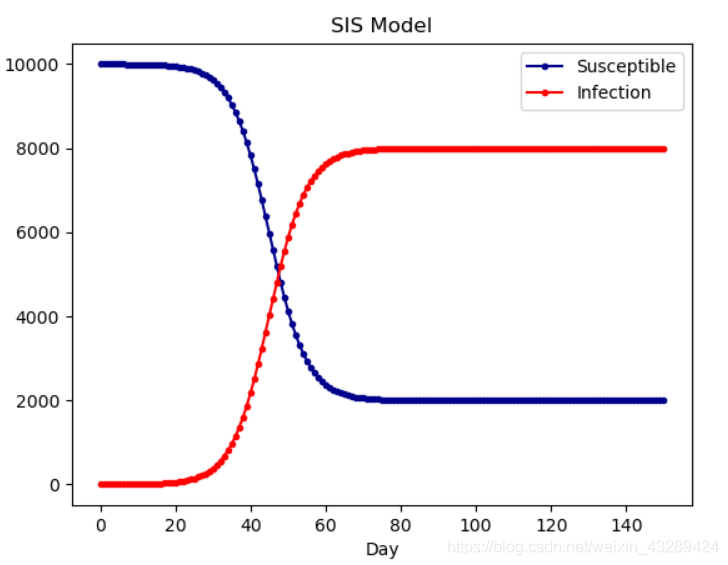
SIR 模型
SIR 中的 R 为 Removal(移除,即:康复者),本模型旨在研究 S、I、R 三者之间的关系。
开始阶段,所有人均为易感者。当一部分人接触到病毒后,变成了感染者。感染者治疗痊愈后,从感染者中移除,变为康复者,并且拥有永久免疫能力。
三者变化关系如下:
模型特征
该模型的前提假设条件:
- 一段时间内总人数 N 是不变的,也就是不考虑新生以及自然死亡的人数
- 从 S 到 I 的变化速度 α、从 I 到 R 的变化速度 β 也是保持不变的
- 移除者不再被感染
模型特征如下: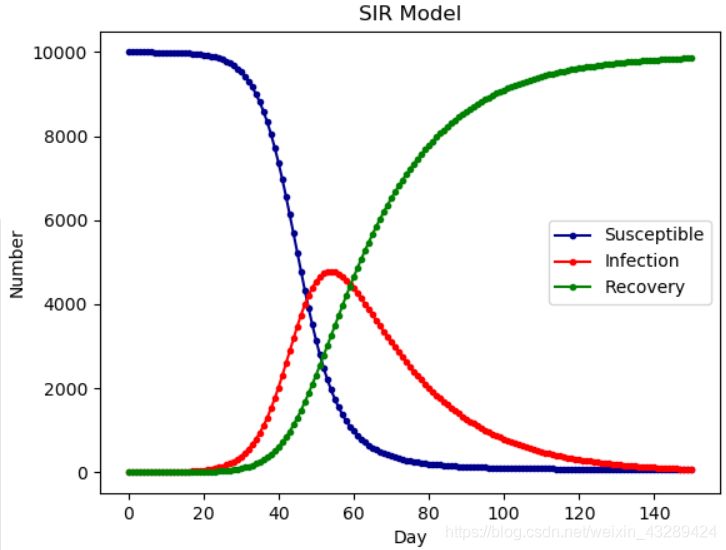
SIRS 模型
与SIR不同在于:康复者的免疫力是暂时的,康复者会转化为易感者
模型特征
模型特征如下: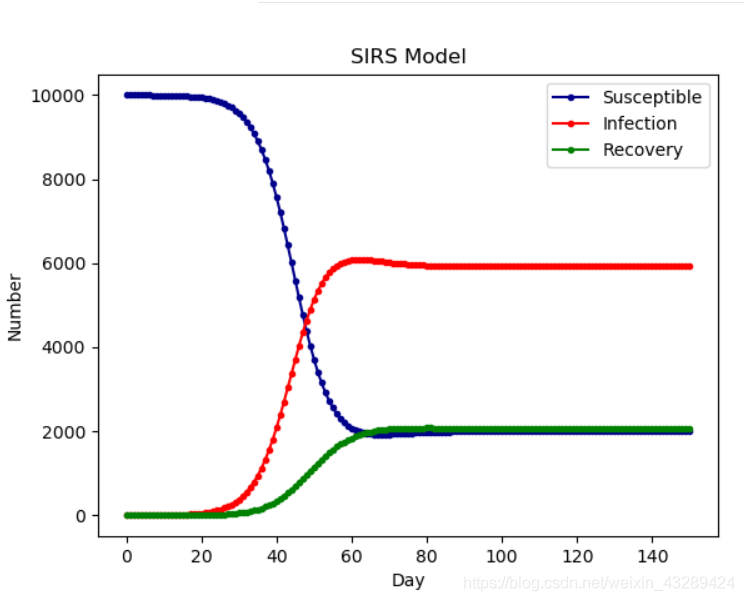
SEIR 模型
在其他模型的基础上,加入传染病潜伏期的存在,康复者
模型特征如下:
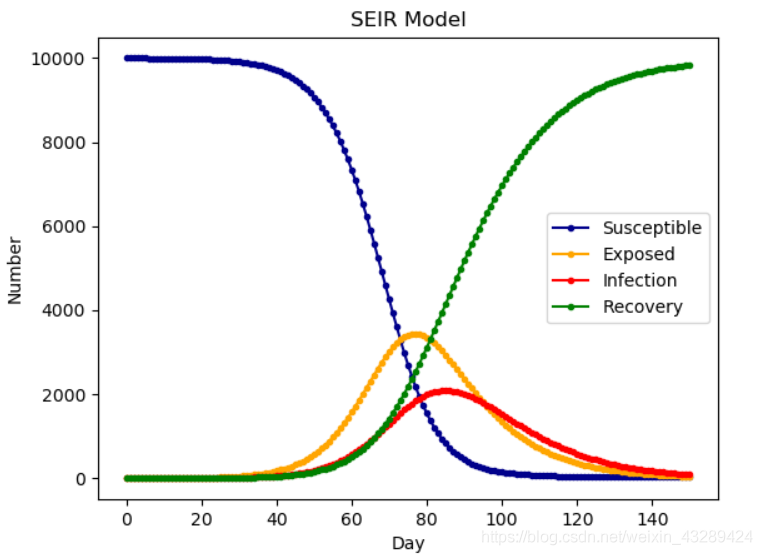
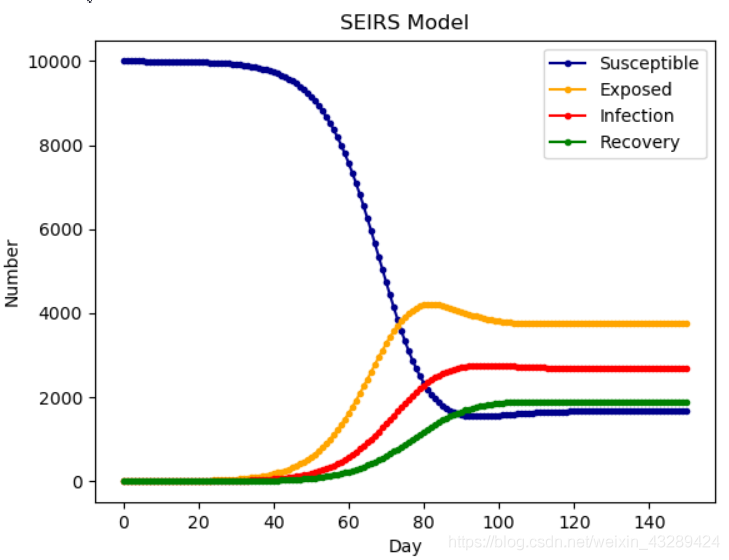
SEIRS 模型
与 SEIR 不同的在于:加入传染病潜伏期的存在,并且免疫力为暂时的,康复者会转化为易感者
模型特征如下:
PS: 后续会对 gossip 的具体实现部分进行补充!
内容参考列表:
[1] https://zhuanlan.zhihu.com/p/41228196
[2] https://blog.csdn.net/weixin_43289424/article/details/104214637


